spirales diverses et variées fin juillet 2017

Continuer à chercher...
D'abord, regarder des spirales suite au visionnage d'une video sur zêta.
Parfois, l'angle entre deux côtés successifs est constant, parfois, c'est la longueur du côté qui l'est. Bien-sûr que ça se pourrait que deux polygones ayant le même nombre de côtés, avec des côtés de longueurs proportionnelles 2 à 2, et d'angles égaux 2 à 2, ayant notamment comme plus grand côté un côté de longueur 1 (allant de l'origine au point d'abscisse 1 de l'axe réel) et des côtés de plus en plus petits de tailles les images des entiers successifs par une certaine fonction, se referment tous les 2 sur 0.
Ce qu'il faudrait comprendre, c'est pourquoi les côtés ont forcément pour longueurs les inverses des racines carrées simples des entiers successifs et pas les inverses des racines cubiques, ou les inverses des racines quartiques ou les inverses des racines quintiques, ou même les inverses des racines 3.14-tiques (!).

Ces polygones acceptables font un peu penser à des "duals" de la spirale de Théodore, dont tous les côtés valent 1 et dont les segments vers l'origine de la spirale sont de longueurs les racines carrées des entiers successifs. Là, ce sont les côtés des polygones qui doivent avoir pour longueurs les inverses des racines (carrées possiblement mais impossiblement cubiques, quartiques, etc) des entiers successifs.

L'ange de la géométrie et le démon de l'algèbre, qu'ils disaient... Encore faudrait-il avoir une très bonne imagination visuelle. Se pourrait-il que le polygone à côtés de longueurs décroissantes associé à Z'1, dont les côtés seraient plus longs un à un de tous les côtés de Z1 mais dont les angles seraient identiques à ceux de Z1, aboutisse aussi, au terme du chemin, au point 0 ?
On pense à cela suite au visionnage de la video dont on a shooté des images en lien avec l'idée énoncée là.
Si deux tels polygones ne pouvaient exister sous prétexte qu'ils ne pourraient tous deux "ramener à zéro" en ayant des côtés en rapport double l'un de l'autre (pour 2/3 / 1/3) ou bien en rapport quadruple l'un de l'autre par exemple (pour 4/5 / 1/5) ou en rapport p-1 l'un de l'autre (pour p-1/p / 1/p), alors peut-être que les seuls polygones acceptables seraient ceux pour lesquels le rapport des côtés est de 1 puisque 1/2 = 1 - 1/2.

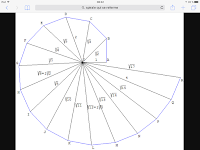
Sur les screenshots, s est le point jaune et zeta(s) est le point vert.